Determinare se esistano relazioni tra eventi che - si suppone - sono in qualche modo legati è un tema che nella scuola, in tutti gli ordini, assume fondamentale importanza. L’analisi dei dati è infatti un argomento che andrebbe trattato trasversalmente e utilizzato quale strumento comune per tutte le discipline.
La parola “relazioni” ha un posto estremamente importante nelle Indicazioni Nazionali, tra gli obiettivi troviamo:

Obiettivi di apprendimento al termine della classe:
terza della scuola primaria	quinta della scuola primaria	terza della scuola secondaria di primo grado
Relazioni, dati e previsioni		Relazioni e funzioni
Leggere rappresentare relazioni e dati con diagrammi, schemi e tabelle	Rappresentare relazioni e dati e, in situazioni significative, utilizzare le rappresentazioni per ricavare informazioni, formulare giudizi e prendere decisioni	Interpretare, costruire trasformare formule che contengono lettere per esprimere in forma generale relazioni e proprietà
		Usare il piano cartesiano per presentare relazioni e funzioni empiriche ho ricavato da tabelle e per conoscere in particolare le funzioni del tipo y=ax, y=a/x, y=ax2, y=2n e i loro grafici e collegare le prime due al concetto di proporzionalità

 

In questo contributo mi soffermo in particolare sulla difficoltà che gli studenti riscontrano nell’individuare, qual ora possibile, il tipo di funzione che possa rappresentare un certo tipo di fenomeno (fisico, economico, biologico o altro).
Occorre dunque evidenziare il fatto che si possono considerare diversi tipi di relazione in grado di legare due grandezze, anche nel caso particolare in cui al crescere (o al decrescere) della prima variabile cresce (o decresce) anche la seconda variabile.
Inoltre bisogna precisare che non solo una dipendenza lineare o una relazione di proporzionalità diretta gode della caratteristica appena descritta ma esistono tante alternative.
È certamente vero che se due grandezze sono tra di loro direttamente proporzionali al crescere della prima cresce anche la seconda; tuttavia tale definizione risulta riduttiva e incompleta se si parla di proporzionalità o di linearità.

Un esempio? Basti pensare all'altezza in funzione del tempo nelle tabelle di crescita dei bambini. Con il passare del tempo i valori misurati diventano maggiori ma, certamente, non in maniera lineare e, dunque, dopo pochi mesi di crescita velocissima seguirà uno sviluppo sempre più lento. Interessante notare che nei primi tre mesi la crescita del peso e dell’altezza potrebbe effettivamente sembrare lineare; tale tendenza tuttavia viene presto disattesa da una curva sempre più lenta.
Questo tipo di rapporto tra grandezze a scuola si studia frequentemente, per esempio sotto forma di grafico spazio/tempo. Ciò che, secondo me, deve essere evidenziato, è che stiamo trattando una relazione tra due grandezze completamente diverse tra loro: qualcosa che si misura con le unità di misura del tempo (secondi, minuti, ore, mesi, anni) con qualcos’altro che si misura in chili oppure in metri.
In questo contesto mi pare interessante citare un brano di un notissimo libro di Nassim Nicolas Taleb "Il cigno nero" in cui l'autore propone un'immagine in cui viene presentata una successione di punti in un grafico di coordinate cartesiane.

"Poniamo che la vostra insegnante delle superiori vi chieda di ampliare la serie di punti. Con un modello lineare, ossia usando un righello, potete disegnare solo una linea retta, un'unica linea retta tra il passato il futuro. Il modello lineare unico. Da una serie di punti può essere proiettata solo una linea retta. ma la cosa può diventare più complicata. Se non vi limitate una linea retta, potete scoprire che esiste un'enorme famiglia di curve che possono collegare i punti. Se proiettate dal futuro in modo lineare fate proseguire una tendenza, ma le possibili deviazioni future dal corso del passato sono infinite."

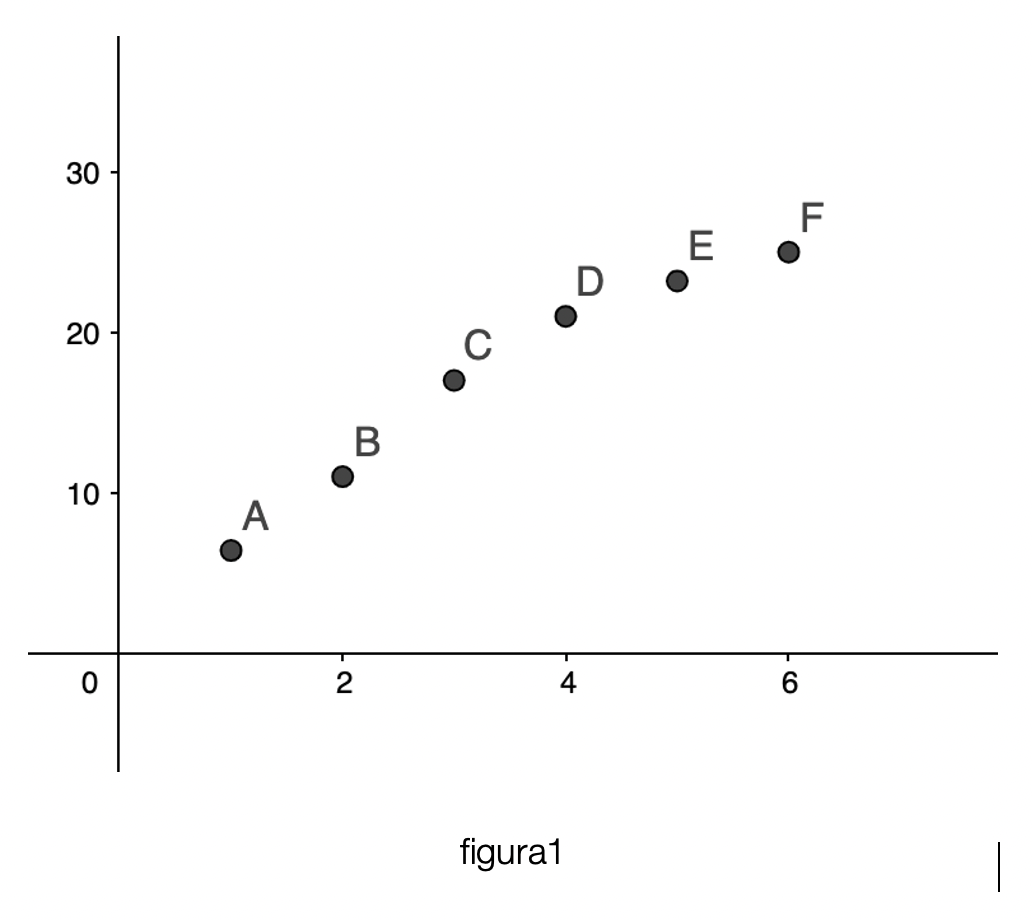
Possiamo esemplificare quanto affermato nel testo di Taleb immaginando una successione di punti ricavata dall’osservazione di un certo fenomeno, come in figura 1.

 

Usando un righello - oppure GeoGebra, usando il comando regressione lineare - potremmo ottenere la seguente retta (figura 2).

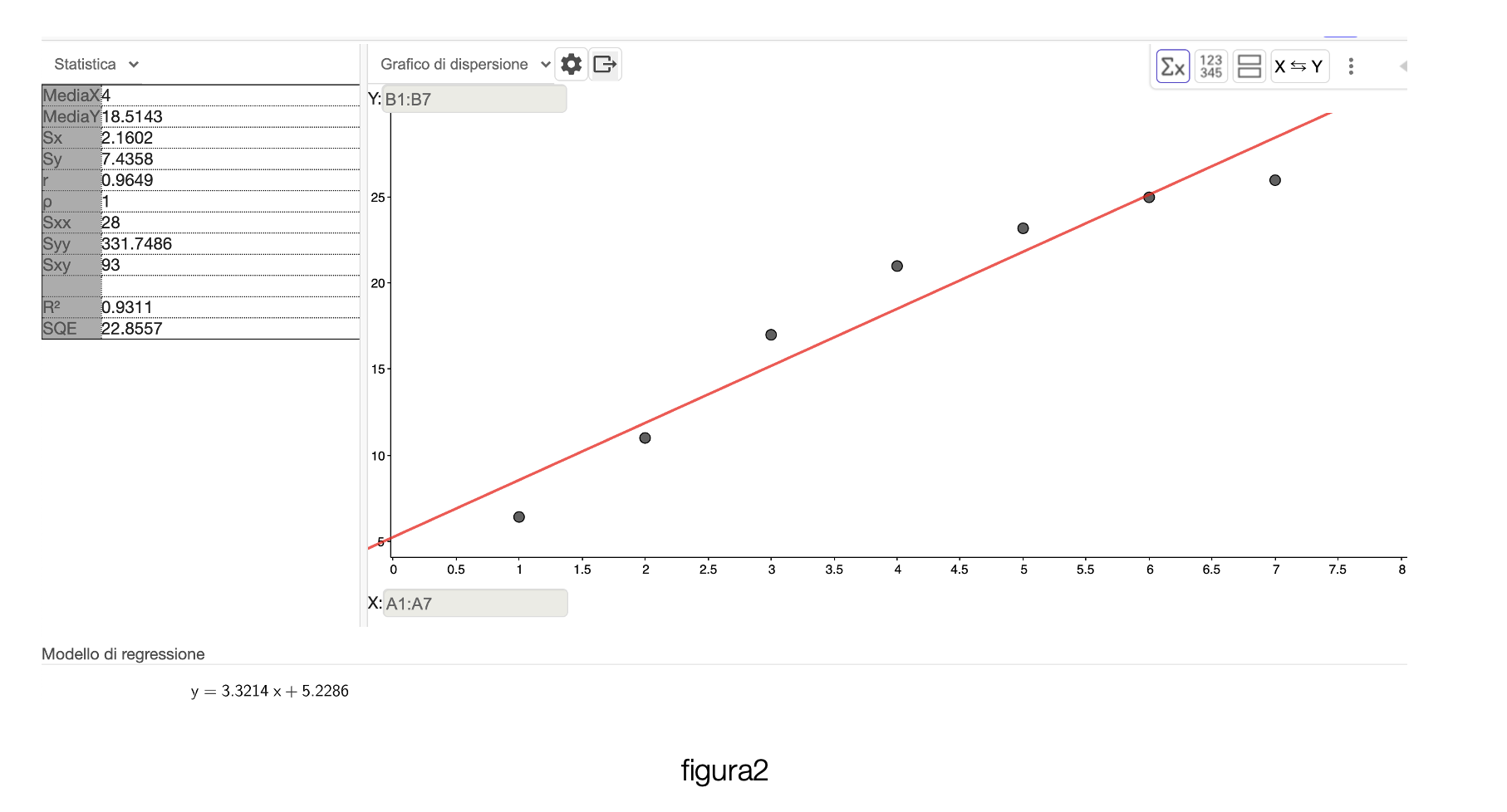
La domanda che l’insegnante del testo di Taleb sta ponendo ai propri studenti ha a che fare in qualche modo con l’azione del prevedere. Nel momento in cui decidiamo che i punti debbano essere uniti da una retta - la retta individuata dal software è un’ottima approssimazione sulla base dell’analisi fornita dai dati statistici elaborati nella parte destra della figura2 - abbiamo deciso di immaginare che anche nel futuro la crescita sarà costante.
È importante dunque sottolineare che la nostra scelta di unire i puntini attraverso una retta potrebbe apparire forse come la più naturale e intuitiva; tuttavia è arbitraria. Inoltre il solo fatto di avere unito i puntini è già di per sé una forzatura in quanto rappresenta la volontà di determinare un andamento ben preciso. Tra un punto ed un altro non sappiamo cosa sia effettivamente  successo: se non ci sono ulteriori punti vuol dire che non ci sono osservazioni sperimentali.
In linea teorica tra un dato ed un altro potrebbe essere sfuggito un valore clamoroso (nella figura 3 è stato inserito un'ulteriore riga che indica le coordinate del punto che vediamo completamente disallineato dagli altri) che cambierebbe la plausibilità del modello matematico scelto.

 

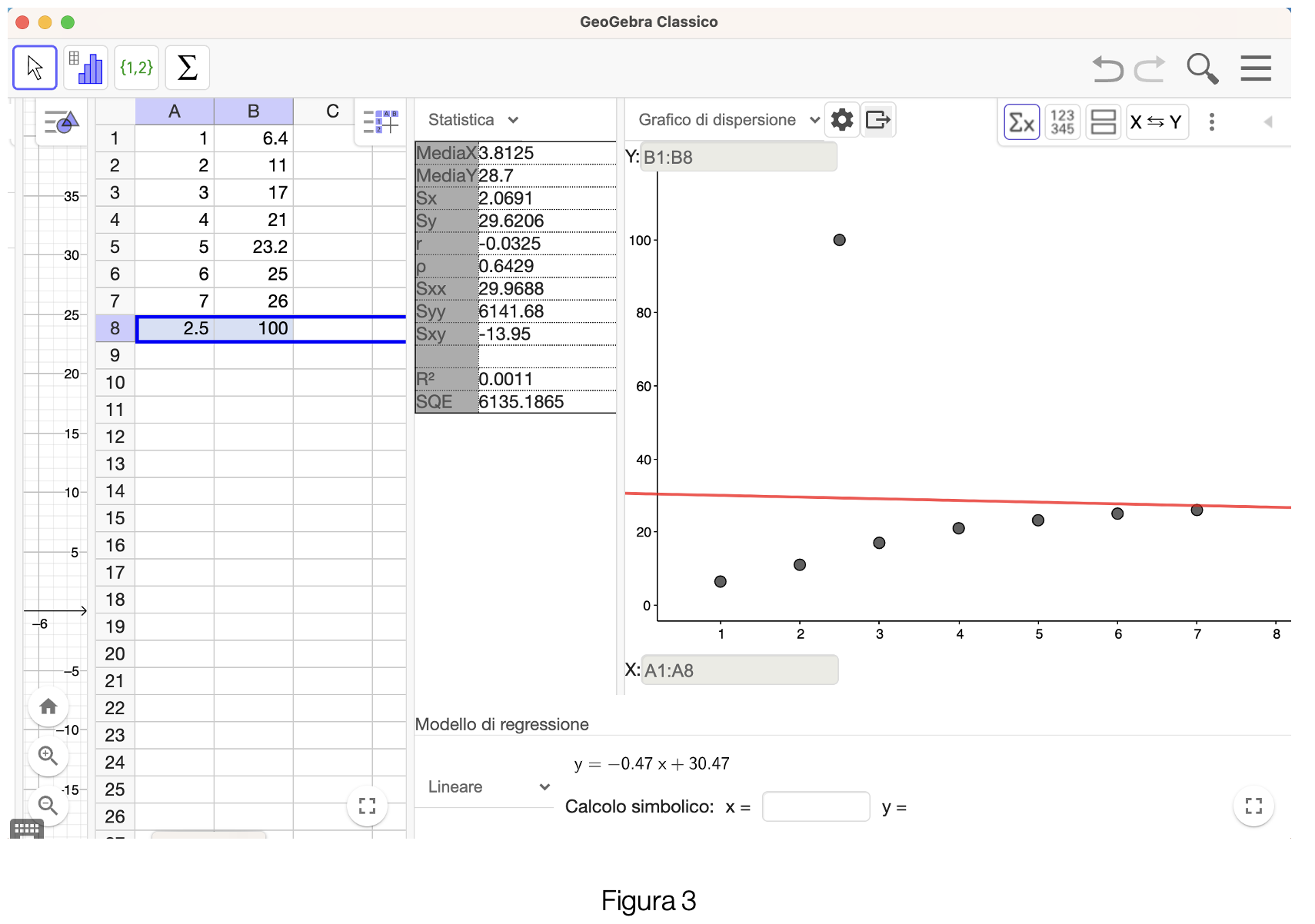
Potremmo anche scegliere altre curve.
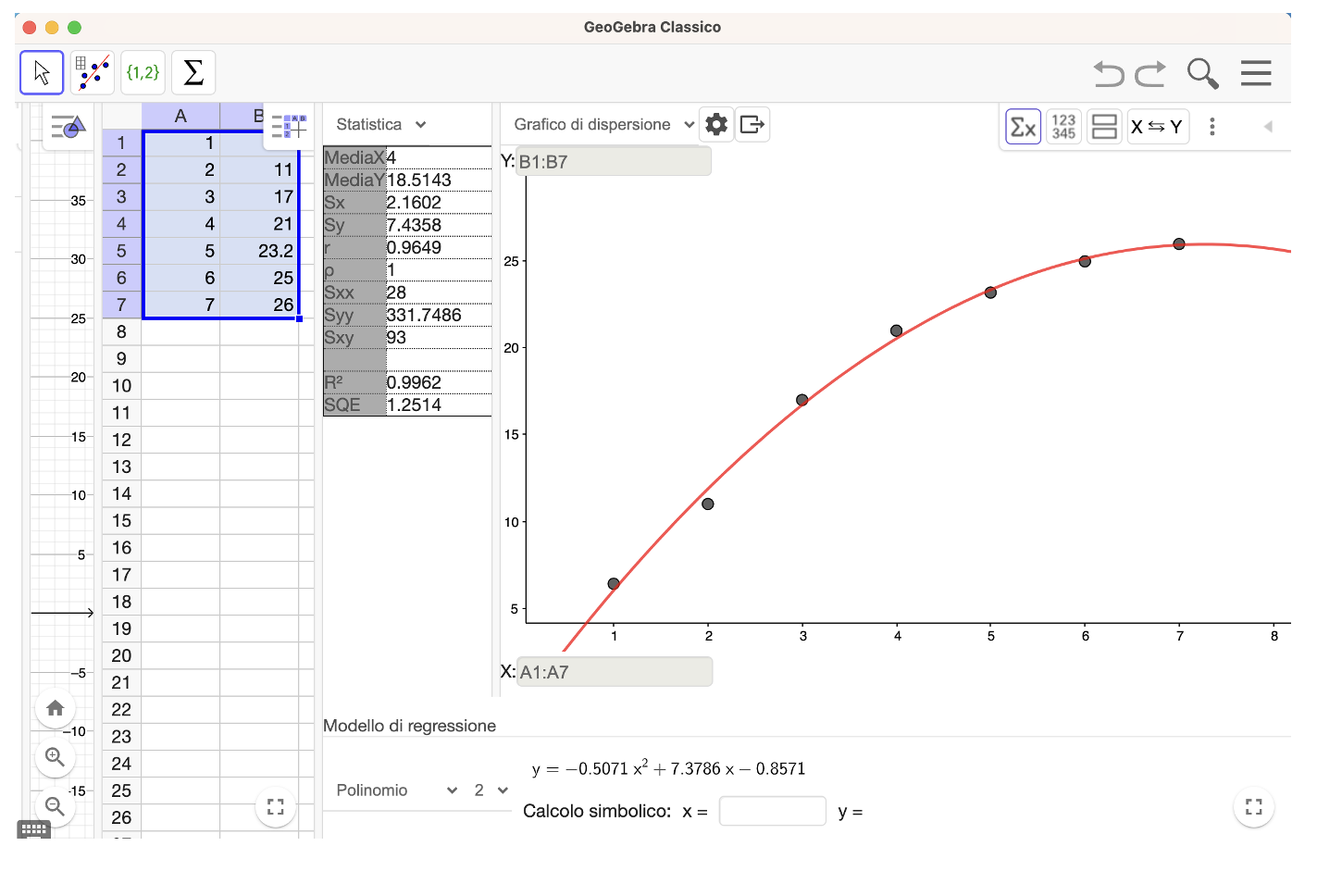
Nella figura 4 abbiamo scelto un andamento parabolico. In tal caso si potrebbe dire che abbiamo una visione pessimista del fenomeno e i dati statistici ci confermerebbero peraltro questa scelta. Stiamo supponendo che dopo una veloce crescita ci sarà, inesorabilmente, una repentina discesa:

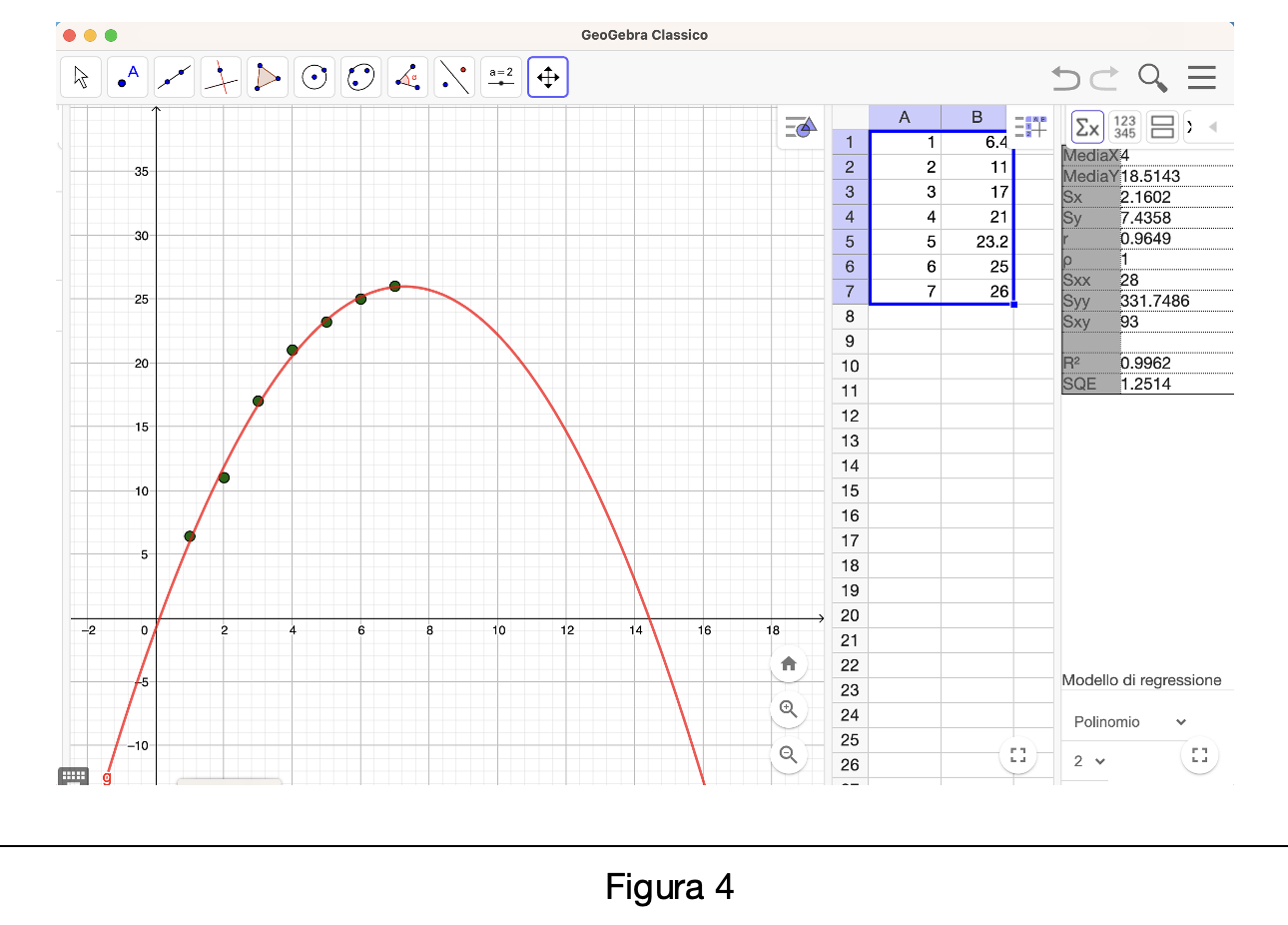
In questa ulteriore prova (figura 5) abbiamo provato ad utilizzare una funzione logaritmica:

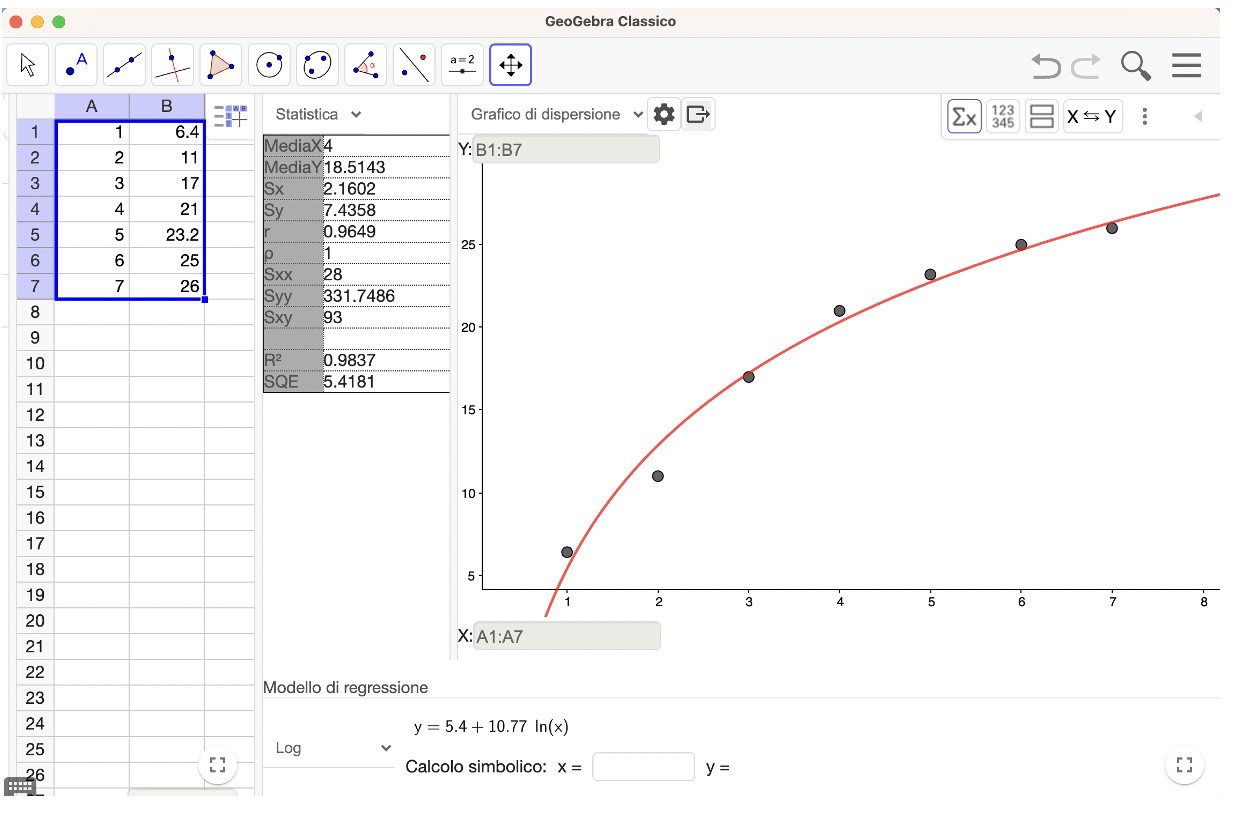
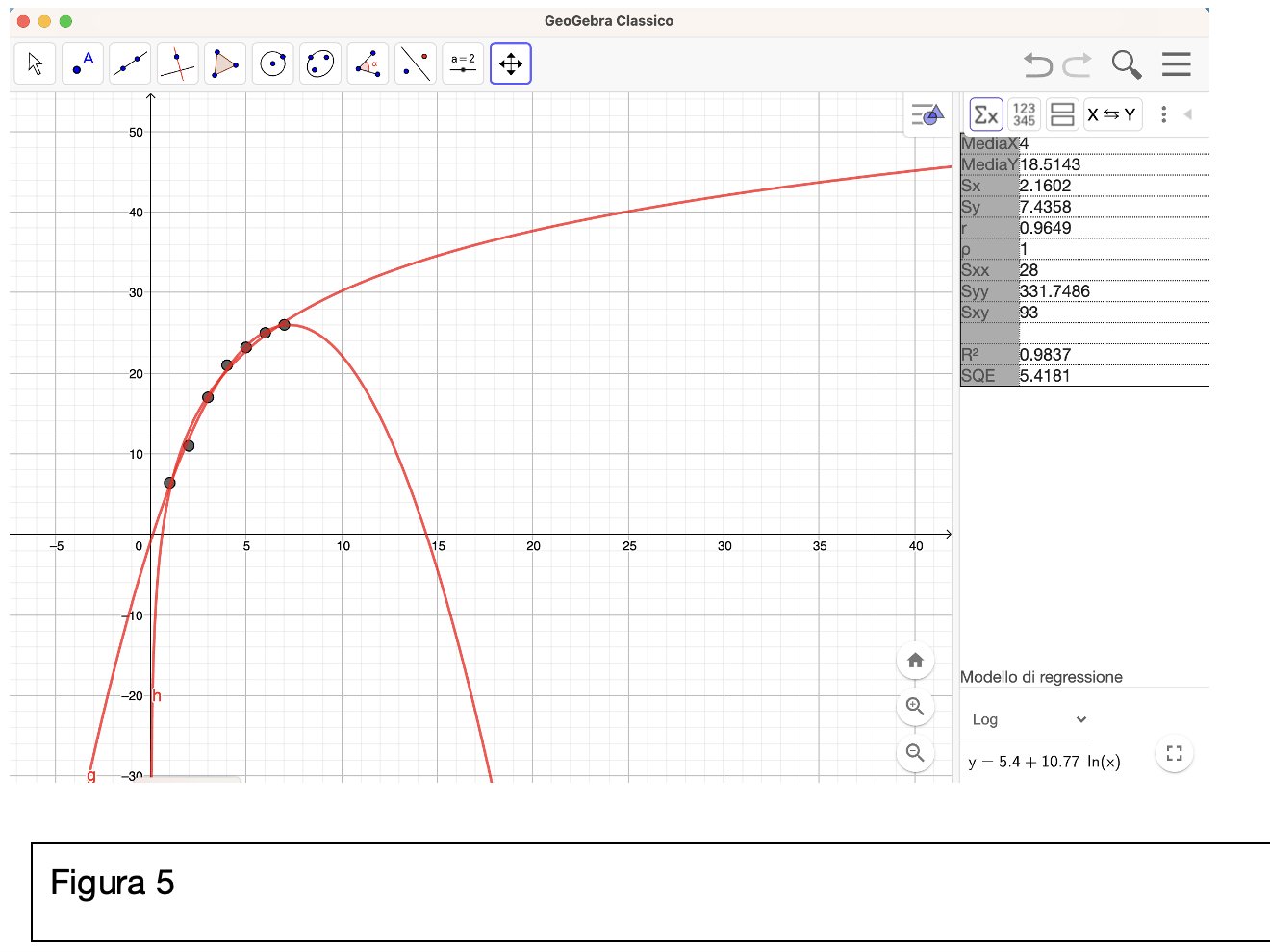
A differenza della funzione polinomiale di secondo grado, quest’ultima è sempre crescente pur con sempre minore velocità. Se si trattasse di una previsione di tipo economico probabilmente sentiremmo i notiziari parlare in maniera allarmante di “crescita in calo”. Tuttavia, se si trattasse dell’andamento dei risultati elettorali di un partito politico potremmo parlare di prospettive di crescita incoraggianti.
Riflettere su tali situazioni può essere un'occasione per avvicinare gli studenti ad uno studio della matematica contestualizzato anche nella attualità politica, sociale ed economica.
In effetti i dati considerati non sono dati casuali ma tratti dal sito "demopolis". Come si può osservare i punti sono stati uniti e non ci sono assi cartesiani che ancorino i punti ad un sistema di riferimento.

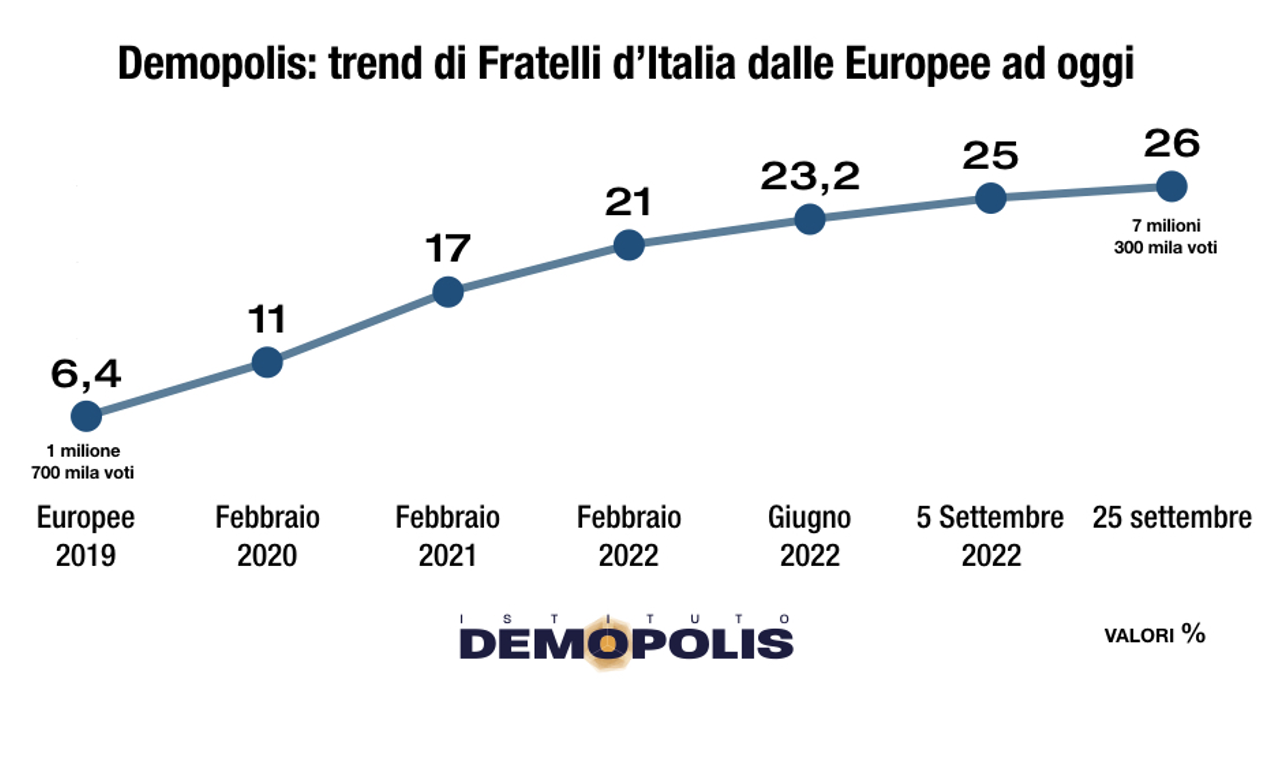
D’altra parte, anche con gli assi cartesiani, in base alla rappresentazione che ne si vuole dare, l’andamento degli stessi valori può apparire molto differente come si osserva nelle figure

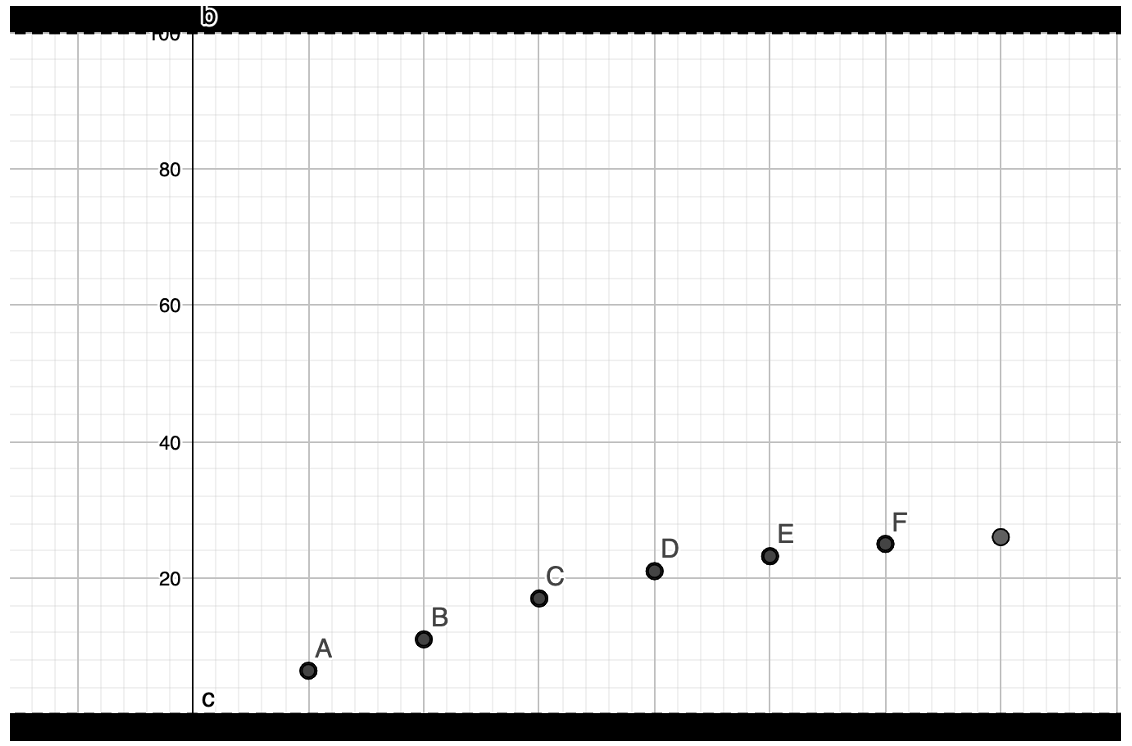
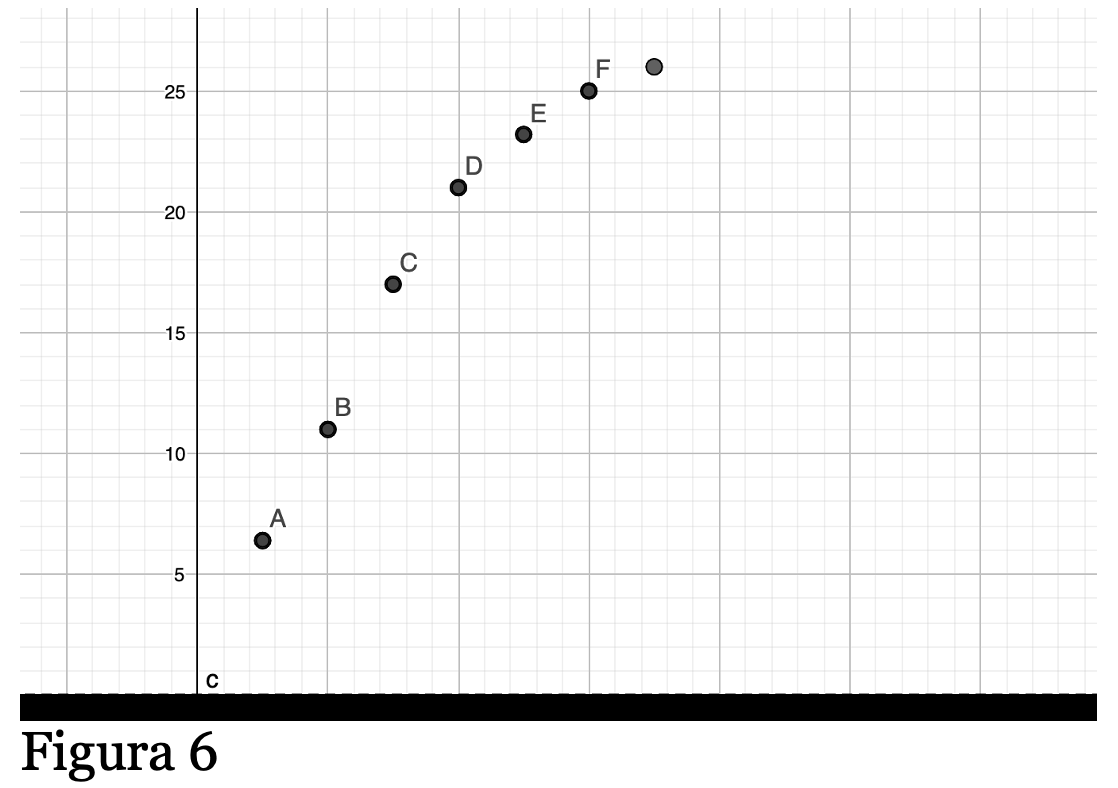
Per concludere: ritengo fondamentale che gli studenti siano abituati ad osservare i fenomeni attraverso analisi quantitative; ritengo altrettanto importante evitare la tentazione di vantare una oggettività che, spesso, semplicemente, non è possibile né opportuna.I dati raccolti, specie quando si parla di scienze sociali, di economia e di politica, difficilmente sono utili a prevedere un futuro anche molto prossimo.
Lo studio (o anche semplicemente la descrizione) di funzioni più complesse rispetto a quella lineare può essere una buona occasione di riflessione per l’analisi, attraverso strumenti matematici, di fenomeni complessi (appunto!) con più lucidità e maggiore consapevolezza.