Com’erano le tracce della maturità del compito di matematica di quest’anno? C'è chi ha detto facilissime, chi impossibili.

Il primo problema a uno sguardo veloce mi sembrava meno impegnativo del secondo, forse con meno calcoli e meno lungo. I quesiti richiedevano molto spesso la conoscenza di argomenti che si fanno (se si fanno) negli anni precedenti alla quinta, alcuni addirittura al biennio e non è affatto detto che i ragazzi se li ricordino. Il numero 1, per esempio, poteva essere risolto in maniera elegante se ci si vedeva Talete (che si fa all’inizio del liceo), altrimenti la soluzione con la geometria analitica era lunga e complessa.

La domanda giusta da fare, secondo me, non è com’erano le tracce. Che poi, com’erano per chi? Per un laureato in matematica? Per i docenti? Per una forma di oggettività che non può esistere? Quanto piuttosto: gli studenti sono mediamente in grado di risolvere questo tipo di problemi e quesiti? Personalmente sono convinta che molti degli studenti che hanno dovuto  affrontare questo scritto si siano trovati, spesso “incolpevolmente”, in serie difficoltà (causate anche dal clima di tensione e ansia che caratterizza il compito di matematica in maniera significativamente maggiore rispetto alle seconde prove degli altri indirizzi, e questo sarebbe un altro tema importante su cui riflettere). Per risolvere questa tipologia di problemi, bisogna lavorarci a lungo, arrivare ad avere una familiarità non banale con determinati argomenti, riuscire a cogliere relazioni e collegamenti, padroneggiare non pochi strumenti matematici.

Tutto questo si può  ottenere se si dedicano diversi mesi, in maniera secondo me quasi esclusiva e sicuramente continua ed emotivamente serena, allo svolgimento e alla comprensione profonda di prove e contenuti che si portano dietro una complessità che a scuola è sconosciuta. Ed è sconosciuta per un sacco di motivi diversi, a cominciare da questioni di tempo. Se pensiamo di poter portare un’intera classe ad affrontare questo genere di verifica svolgendo ogni tanto una prova d’esame degli anni precedenti, avendo 4 ore settimanali di matematica a disposizione (quando va bene) in cui si studia, spesso male e in fretta, un programma praticamente di Analisi 1 (certo, con molte meno dimostrazioni, ma con lo spauracchio di uno scritto finale che, per certi versi, è ben più complesso e lungo delle prove previste per questo esame a livello universitario), dovendo anche riprendere o affrontare per la prima volta elementi di calcolo combinatorio, calcolo delle probabilità e geometria dello spazio, stritolati tra pcto e orientamento che sottraggono tempo, energia e concentrazione, allora siamo fuori dal mondo.  Il rischio (praticamente una certezza) è quello di restare inevitabilmente sulla superficie dei contenuti, dando spazio principalmente ad aspetti procedurali e non al senso e a una reale comprensione di argomenti delicati e impegnativi. Per non parlare del fatto che contemporaneamente gli studenti hanno tante altre discipline da studiare, con interrogazioni e compiti in classe che si susseguono senza tregua, perché il fine ultimo della scuola resta “mettere voti”, mica costruire conoscenza e pensiero! Motivo per cui lo studio individuale della matematica viene spesso interrotto per dare spazio al resto.

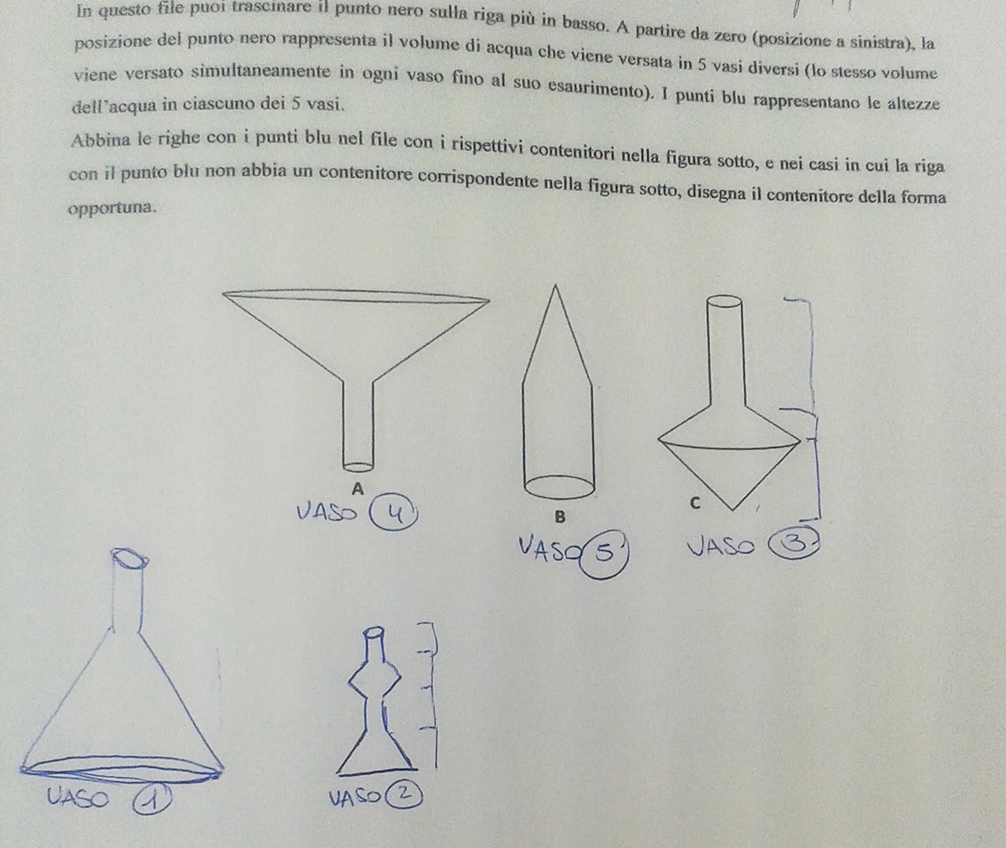
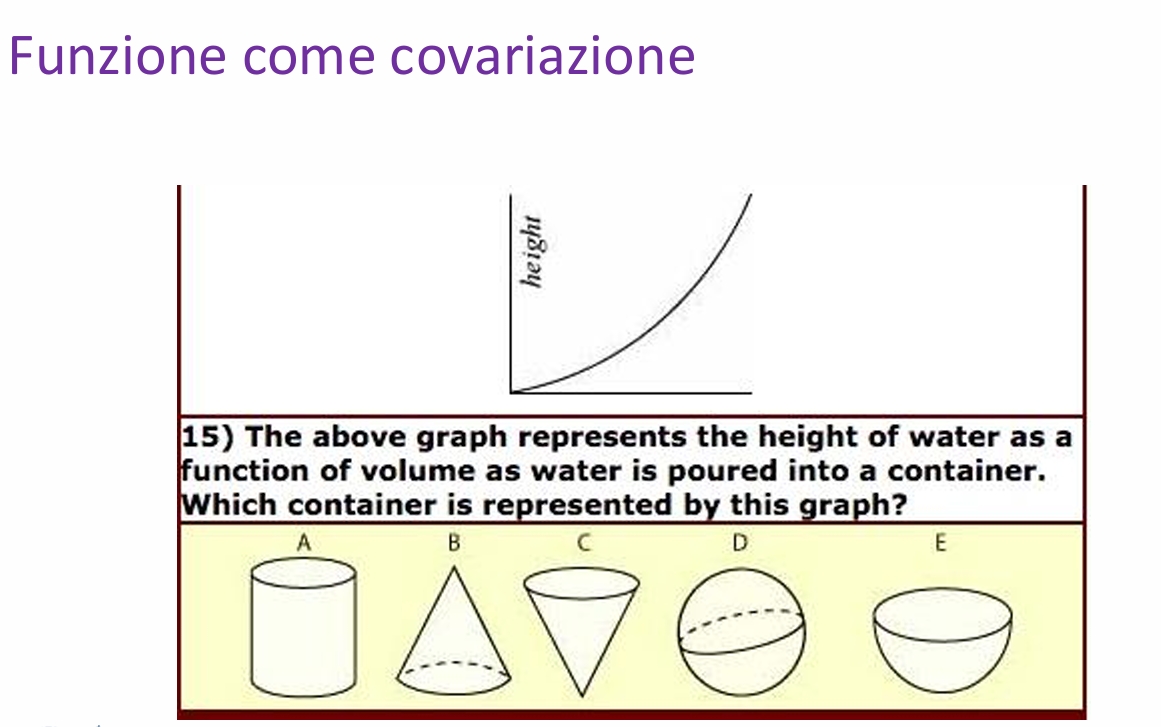
Inoltre mi domando, il tipo di preparazione che si porta avanti per affrontare lo scritto finale, non è penalizzante rispetto aspetti significativi degli argomenti affrontati?  Mi spiego meglio, quanto viene fuori in classe, per esempio, il tema della covariazione nello studiare le funzioni? Penso a software potenti e belli come dynagraphs (e per lo più sconosciuti in classe),  che ti consentono di vedere le funzioni in maniera dinamica e di cogliere aspetti fondamentali che, inevitabilmente, non emergono nella visione statica a cui siamo abituati. E penso ai quesiti sorprendenti e stimolanti che si possono proporre adoperando questo tipo di approccio, dove non devi ricordare formule, ma aver capito veramente cos’è una funzione e descriverla nell’ottica della covariazione (vedi immagini tratte dalla presentazione della professoressa Giulia Lisarelli - Università di Pisa: Esperienze di ricerca qualitativa in didattica della matematica). Per chi voglia approfondire, consiglio questi due articoli:

• G. Colacicco, G. Lisarelli & S. Antonini, (2017), Funzioni e grafici in ambienti digitali dinamici. In Didattica della Matematica: dalla ricerca alle pratiche d'aula, 2, 7-25. 
• L’uso del movimento nell’esplorazione e risoluzione di attività con grafici dinamici -  G. Lisarelli - L’insegnamento della Matematica e delle Scienze Integrate. Vol. 42 A-B N. 3 - maggio - giugno 2019

Tornando al compito, come finisce di solito? Non prendiamoci in giro, quasi sempre le soluzioni, o parte di esse, in qualche modo arrivano, per evitare che la maggior parte degli studenti consegni il foglio in bianco  o quasi. Negli ultimi anni poi le prove sono accompagnate da citazioni, frasi in latino, grafici creativi e poligoni dai nomi poetici, a voler in qualche modo provare ad andare in una direzione che colleghi la matematica al mondo umanistico. Pur ritenendo che tali “innesti” non siano dei distrattori per gli studenti, da docente (di matematica) li trovo particolarmente fastidiosi per diversi motivi. Le parole di Hilbert, per esempio, «La matematica non conosce razze o confini geografici; per la matematica, il mondo culturale è una singola nazione», sono sicuramente belle, ma decisamente stridenti rispetto a perle che provengono dall’attuale Ministero dell’Istruzione (e del merito), come quel “Solo l’Occidente conosce la storia” che abbiamo letto con grande scoramento nella proposta di Nuove Indicazioni Nazionali . E mentre leggo Cartesio come preambolo al primo problema, «La ragione non è nulla senza l’immaginazione»,  non posso fare a meno di pensare che quasi sempre la matematica del liceo scientifico è presentata in classe in una maniera che più arida non si può. Altro che immaginazione, se provi a proporre di risolvere un problema con una strategia che non è quella che ha in testa il tuo professore, ecco che parte la penna rossa, a prescindere. Peccato, quindi, che la scuola italiana, alle superiori più che mai, nei licei all’ennesima potenza, non parliamo poi dei licei “d’elite”, che lì si forma la futura classe dirigente, che deve saper obbedire, mica essere capace di complessità, proceda in una dimensione che ragiona ferocemente quasi esclusivamente per compartimenti stagni. Figurarsi se nel quotidiano delle nostre lezioni saperi scientifici e saperi umanistici possono incontrarsi. Insomma, un grande bluff, fumo negli occhi e nulla di più. Queste tracce, che si portano dietro contraddizioni, incoerenza e inganno, dimostrano, dal mio punto di vista, soprattutto che chi le ha proposte è lontano anni luce dalla verità della scuola italiana e dall’ora di matematica che quotidianamente si vive in classe. Non posso fare a meno di chiedermi, allora, esattamente a che serve tutto questo? A imparare la matematica? Manco di striscio, al massimo a detestarla, visto lo stato di paura, stress e frustrazione che genera tutto ciò negli studenti, portando alcuni di loro a evitare accuratamente nel futuro una scelta universitaria che contempli esami di matematica (e parliamo di studenti che scelgono lo scientifico quasi sempre per passione nei confronti della principale disciplina d’indirizzo). A stabilire se una ragazza o un ragazzo sono maturi? Ma seriamente lo pensiamo? E di grazia, dove sarebbe la maturità? Nel copiare un compito senza dare troppo nell’occhio? E quelli che hanno comunque studiato tutto l’anno, tutti gli anni, provando a fare quello che potevano, ma il compito non riescono a farlo, anche perché  così lontano dalla maggior parte di problemi e esercizi con cui si sono confrontati in classe, sono quindi immaturi? E perché questi compiti non possono essere svolti in un clima sereno, cooperando apertamente? Non è forse una preziosa e bella dimostrazione di maturità saper lavorare insieme, aiutarsi a vicenda? Magari con le formule a portata di mano, visto che non si capisce perché uno le debba conoscere a memoria. Oppure ci piace l'accoppiata Matematica e Sadismo di cui ci parlavano i ragazzi di Barbiana in Lettera a una professoressa? Ma se la maggior parte dei nostri studenti di liceo scientifico, e non solo, ha un professore privato di matematica, due domande forse non dovremmo farcele? O va bene accettare che tutto questo sia la normalità, facendo finta di niente? Per quale motivo la scuola deve abituare studentesse e studenti a bugie, ipocrisia e finzione? Siamo alle solite, la matematica è bellissima, è potente, è formativa, è un patrimonio culturale dell’umanità, ma così diventa escludente, distante, odiosa, respingente, non democratica. Tanto che, oggi come oggi, se un alunno di terza media mi dicesse che la sua materia preferita è la matematica, quello che gli risponderei è: fantastico, allora non iscriverti al liceo scientifico!