Una premessa

Seguo come tutor progetti di scienze nelle scuole e ne ricavo anche materiali interessanti per la mia ricerca epistemologica su come pensano le/i bambini. Questa volta però sono stato coinvolto in una discussione che riguarda come pensano le/gli insegnanti, in particolare quelli di matematica della scuola media; “come pensano” è riferito al contesto della didattica, che è una variabile importante nello sviluppo delle competenze di cittadinanza di tipo matematico-scientifico.

Oggetto della discussione è l’utilizzo didattico del geopiano, uno strumento che ha illustri natali perché è tra le proposte di Emma Castelnuovo. Non l’ho mai incontrata personalmente, purtroppo, e quindi la mia riflessione critica non riguarda le sue proposte, ma l’uso che di fatto se ne fa nelle scuole.
Il geopiano [vedi immagine 1] si può facilmente costruire anche con materiali poveri: una tavoletta di legno rettangolare in cui sono infissi equidistanti dei chiodini disposti in file parallele ai lati. Anche ai non matematici verrà subito in mente, per memoria di scuola, il “piano cartesiano”. “Verrà in mente”, ma, se vogliamo entrare nel contesto matematico, il geopiano diventa un modello materiale del piano cartesiano se:
a) vengono identificate come “asse x” e “asse y” due direzioni nel piano (non necessariamente perpendicolari);
b) viene scelta una unità di misura (convenzionalmente la distanza tra un chiodino e l’altro, misurata lungo i due assi.
L’ultima specificazione è importante perché la distanza tra due chiodini in diagonale è maggiore. Se la distanza lungo gli assi è 1 unità, questa diagonale si ricava con il teorema di Pitagora = 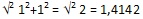… : è un numero irrazionale, con infinite cifre dopo la virgola, difficile da trattare, tanto da richiedere un’estensione dei numeri fuori dal campo dell’aritmetica, che ha creato problemi proprio nella misura delle lunghezze tanto da mandare fuori di testa… i pitagorici).
Se l’ipotesi che suggerisce l’uso del geopiano in un contesto didattico è che l’oggetto possa essere un modello materiale di un piano della geometria, ci si deve prima di tutto porre il problema del modello, ovvero se l’oggetto materiale ha caratteristiche corrispondenti (isomorfe) alla struttura matematica, geometrica in questo caso, che dovrebbe rappresentare, ma soprattutto quali caratteristiche del modello NON vi corrispondono e che quindi non sono pertinenti al discorso geometrico. Per un matematico questo non è un problema: per entrare nella comunità dei matematici è stato iniziato all’astrazione, al dovere di dimenticare, nell’uso degli oggetti che costituiscono il suo campo di azione, tutte le caratteristiche che non siano pertinenti alla loro definizione valida in quel contesto. Questo campo di azione è un “gioco linguistico” nel senso che dà al termine Wittgenstein, ovvero di situazione sociale riconosciuta, per cui sono noti i ruoli nelle relazioni di chi vi partecipa e le regole condivise di interazione comunicativa.

Le scienze sono giochi linguistici, con regole più stringenti rispetto alla normale convivenza in una comunità sociale, e la matematica ancora di più. Ciò che aumenta in questi contesti è la rigorosità delle “regole del gioco” condivise, che si esprimono in una formalizzazione delle rappresentazioni e del linguaggio. Nel caso delle scienze naturali le rappresentazioni sono “mappe” di un “territorio” reale osservato, e quindi sono vincolate da una coerenza con esso (le previsioni fatte in base alla rappresentazione devono essere confermate dai risultati effettivi osservati nel territorio della realtà); invece nel caso della matematica le rappresentazioni sono inventate indipendentemente dal fatto che (e spesso prima che) esista un territorio di cui siano mappa. In altre parole il territorio di applicazione delle rappresentazioni è inventato quanto la mappa, è un prodotto delle menti umane (un prodotto culturale). Questa caratteristica porta al massimo livello la convenzionalità delle “regole del gioco” e dei contesti di validità. Ne consegue che è possibile giocare a quel gioco con altre persone solo se tutti ne condividono e rispettano le regole. Ovviamente le regole si possono cambiare, ma questo richiede necessariamente che le nuove regole siano negoziate in una dimensione “meta-gioco”, condivise per arrivare a una nuova convenzione, necessariamente rigida finché si sta dentro il gioco.

Tornando all’uso dei modelli: per i matematici è ovvio che cose come il peso, il colore, la conducibilità elettrica, la luminosità, ma anche l’orientamento rispetto allo Zenit o al Nord ecc., che caratterizzano un oggetto materiale come il geopiano, non sono pertinenti alla struttura matematica astratta di cui vuol essere modello e quindi vanno tenute fuori dal campo dell’interazione col modello. Ma se il modello viene proposto come contesto di interazione a persone che non conoscono ancora il gioco linguistico della geometria, e a maggior ragione se si propone loro il modello materiale proprio per introdurvele, è ovvio che si deve tenere conto della loro ignoranza (perché è proprio questo che definisce il ruolo dell’insegnante rispetto alle/agli studenti). Quindi l’errore più paradossale che un insegnante può commettere è dare per scontato con le/gli studenti proprio ciò che loro non sanno e che sono lì per imparare dall’insegnante. In realtà nella mia idea di relazione educativa le/gli studenti imparano non “dall’insegnante” ma “grazie anche a ciò che fa l’insegnante”, ma questo è un altro ulteriore discorso: qui volo più basso e mi limito a segnalare una condizione elementare e preliminare per l’apprendimento: conoscere le regole del gioco che si viene invitati a giocare.

Alcuni esempi

Fatta questa premessa, prendo come oggetto di indagine ed esempio significativo il testo di esercizi proposto dall’insegnante alle/agli studenti di una classe prima media. Inizia con una nota:

NOTA BENE: PER UNITA’ SI INTENDE LA DISTANZA TRA DUE NUMERI SIA SULL’ASSE X, SIA SULL’ASSE Y

Segue il primo esercizio (consiglio di munirsi di foglio a quadretti e di provare).

RAPPRESENTA SUL GEOPIANO I PUNTI (9; 1); (9; 7): QUAL È LA LUNGHEZZA DEL SEGMENTO CHE HA PER ESTREMI I DUE PUNTI?

Un alunno non ha scritto 6 unità, ma ha preso il righello, ha misurato ed ha scritto la lunghezza in centimetri e l’insegnante l’ha ritenuto un errore, immagino con la motivazione che nella nota aveva indicato l’unità come “distanza tra due numeri sull’asse”. Se ci si trova su un piano cartesiano e se il segmento è parallelo a uno degli assi, si può calcolare la differenza tra i numeri come corrispondente alla distanza tra punti estremi del segmento. Anzi basterebbe guardare le coordinate: tra 1 e 7 (coordinate y) c’è una differenza di 6, che corrisponde alla distanza tra i due punti nella direzione y. Ma, se si deve fare riferimento ai numeri per conoscere la lunghezza, perché proprio i numeri nella direzione y invece che nella x? Nell’esercizio non lo si specifica. E poi, se il prof. vuole sapere la lunghezza del segmento, che è sempre la stessa, perché calcolare la distanza tra due numeri, che invece cambiano a seconda di dove è posto il segmento e dell’orientamento che ha, con la mortale complicazione che, se non è parallelo agli assi, saltano fuori numeri irrazionali? Perché non fare ciò che è richiesto fare quando si vuole conoscere la misura di una lunghezza, ovvero misurarla con l’apposito strumento che è il modello materiale per la misura di lunghezza?
L’alunno dunque ha fatto la cosa giusta, nonostante la nota scritta dall’insegnante, che dà per scontata la corrispondenza tra punti e numeri che ne rappresentano le coordinate, rimuovendo tutti i “se”.
L’alunno ha dimostrato saggezza nel non cadere nella trappola di prendere per buono ciò che dice il prof. anche se è sbagliato (ma l’alunno non lo sa), o anche solo incomprensibile; si è fidato più di alcune conoscenze che sente solide e di una facoltà ben sviluppata nei piccoli che è la relazione con il contesto specifico. Dimostra autonomia, o spirito critico, che è una competenza di cittadinanza (non solo scientifica).

Un altro esercizio:

RAPPRESENTA SUL GEOPIANO:
1. UN SEGMENTO CHE HA COME ESTREMI I PUNTI (3; 6) E (4; 6) (SEGMENTO 1)
2. UN SEGMENTO CHE HA COME ESTREMI I PUNTI (3; 5) E (6; 6) (SEGMENTO 2)
3. IL SEGMENTO SOMMA FACENDO IN MODO CHE IL PRIMO ESTREMO SIA IL PUNTO (3; 4) (SEGMENTO 3)

A. QUANTO MISURANO LE LUNGHEZZE DEI TRE SEGMENTI? CHE RELAZIONE C’È TRA IL PRIMO E IL SECONDO SEGMENTO?
B. CHE RELAZIONE C’È TRA IL PRIMO SEGMENTO E IL SEGMENTO SOMMA?

Mi metto nei panni dell’alunno e ...
«Provo a costruire nel geopiano i segmenti 1 e 2, e scopro che non hanno estremi in comune. Arrivato al punto 3. mi imbatto in un problema: nella geometria piana la “somma di due segmenti” è definita solo nel caso che i due segmenti giacciano su una stessa retta e abbiano un estremo in comune (siano “adiacenti”); in questo caso “somma di due segmenti” è il segmento che ha per estremi i due estremi non in comune tra i due segmenti. Allora devo interpretare l’espressione “facendo in modo che”; lo faccio spostando il segmento 1 fino a che il suo estremo (quello più vicino all’asse y spero) sta nella posizione indicata e il segmento 2 fino a che il suo estremo più vicino all’asse y coincide con l’estremo del segmento 1 più lontano dall’asse y. Li ho spostati con delle traslazioni, cioè senza modificare il loro orientamento nel piano. Ma i due segmenti non hanno la stessa direzione, ovvero non sono sulla stessa retta, formano i lati di 2 angoli diversi da un angolo piatto. A questo punto ho due alternative: o rispetto le convenzioni della geometria: in questo caso non esiste una somma dei due segmenti e quindi non posso eseguire l’esercizio (e allora è probabile che il prof. di geometria mi rimproveri); oppure interpreto la “somma dei segmenti”, che sono enti astratti rappresentabili graficamente, come “somma delle misure di lunghezza dei segmenti” che sono invece dei numeri.
Con questo faccio una forzatura delle regole, perché nel contesto convenzionato dell’aritmetica la parola “somma” (tra numeri) indica una operazione del tutto diversa da quella designata dalla parola “somma” (di segmenti) nel contesto convenzionato della geometria. A me sembra che il prof. sovrapponga e confonda le due cose, e quindi può essere che forse non mi rimproveri, ma questa è una mia interpretazione rischiosa. E comunque, se ci avessi azzeccato, d’ora in poi dovrò rispettare le regole della geometria o cercare di interpretare le idee del prof. per fare quello che vuole da me e mi premi… però, se poi vado alle superiori e trovo un prof. che la pensa diversamente?
Ma desso ho un altro problema: in a. e b. che cosa vuol dire “che relazione c’è”? In pratica: che cosa si vuol sentir rispondere il prof.? Secondo me che il primo è la metà del secondo. Ma si riferirà agli oggetti geometrici o alle loro misure di lunghezza? È un problema, perché esistono segmenti che hanno lunghezza doppia di altri, mentre “segmenti doppi” è un’espressione non definita.
Faccio conto sulla confusione del prof. e decido di fare la somma delle lunghezze, ma mi accorgo che ciò che avevo già annotato, che i segmenti 1 e 2 non hanno la stessa direzione, diventa un problema grave, perché il 2 non sta nella direzione di un asse e quindi la sua lunghezza non corrisponde a un numero intero di unità (distanza tra due chiodini solo lungo le direzioni degli assi). Che fare? Idea: faccio ruotare il segmento 2, facendo perno sull’estremo comune fino a che si trova nella stessa direzione del segmento 1, ma devo stare attento a non modificare la sua lunghezza. Fatto… ma così il segmento 2 non ha più l’altro estremo su un chiodino del geopiano, sporge di un pezzo! E allora come faccio a sapere quanto è lungo? L’unico modo che conosco è usare il righello, ma l’altra volta il prof. mi ha rimproverato. Qualunque cosa io faccia, sbaglierò.»
In psichiatria questa conclusione senza via di uscita si chiama “doppio vincolo” e può portare alla schizofrenia. Nel caso dell’alunno sarà uno dei tantissimi che dirà “di matematica non ci ho mai capito niente”.

Ancora un esercizio:

RAPPRESENTA SUL GEOPIANO IL SEGMENTO DI ESTREMI (1; 2) (3; 2).
RAPPRESENTA IL TRIPLO DELLA LUNGHEZZA DI QUESTO SEGMENTO FACENDO IN MODO CHE IL PRIMO ESTREMO SIA IL PUNTO (1; 3)

Una misura di lunghezza, come tutte le misure, può essere rappresentata solo da un numero seguito dall’indicazione dell’unità di misura usata (es. 3 spanne, oppure 12 mm), ma questo tipo di oggetto matematico non ha “estremi”. Forse il prof. nella sua testa pensava alla costruzione di “un segmento che abbia lunghezza tripla del segmento 1 e che abbia l’estremo nel punto…”, ma non l’ha scritto, perciò l’alunno, per rispondere quello che il prof. si attende come risposta “giusta”, dovrebbe saper leggere il pensiero. La confusione tra oggetti, loro grandezze (un oggetto reale ha molteplici grandezze: volume, capacità termica, luminosità, acidità ecc.) e loro misura è una delle carenze che i prof. per tradizione imputano ai bambini. Questo esempio mostra da dove può venire la confusione.

Ancora:

INDIVIDUA I PUNTI A(3;2)  B(6;2)  C(8;8)  D(5;8) CON I CHIODINI E UNISCILI NELL’ORDINE CON LO SPAGO.
QUALI FIGURA OTTIENI?
TROVA GRAFICAMENTE LE MISURE DEI SEGMENTI CHE TI OCCORRONO PER DETERMINARE L’AREA DEL POLIGONO.

Se non si aggiunge, o non si è sicuri che sia già noto, che il “poligono” è la superficie delimitata dai segmenti “uniti”, non si sa di che cosa si stia parlando; se lo si aggiunge, almeno diventa possibile immaginare la superficie delimitata come separata dal resto del geopiano e attribuirle un’identità. Dico “immaginare” perché, come si vede dalla fotografia, non c’è nulla che nel modello materiale identifichi materialmente la superficie del “poligono” fantasma differenziandola dal resto del piano: e allora perché usare un modello materiale?
Il fatto che si possa almeno immaginare tale superficie dipende dal fatto che la “figura” che si forma tracciando i segmenti sia una “spezzata chiusa” e questo dipende dal fatto che si unisca anche D con A altrimenti la “figura” che si ottiene è una linea “spezzata aperta” e non esiste alcuna superficie identificabile se non quella del geopiano.
Nel compito si chiede di “determinare l’area”, che è la misura della grandezza che caratterizza le superfici, ma nel linguaggio del prof. compaiono solo segmenti e le loro misure di lunghezza, che è la grandezza che caratterizza le linee. Questo è significativo, perché un classico delle lamentele delle/degli insegnanti di matematica è che gli alunni “confondono l’area con il perimetro” [immagine 1]. Ora: l’area è la misura dell’estensione a due dimensioni di una superficie, una grandezza che ha a che fare con l’azione del ricoprire (quale tovaglia è abbastanza grande per ricoprire il tavolo? quante piastrelle servono per ricoprire il pavimento?...); invece il perimetro è la misura della lunghezza della linea unidimensionale di contorno di una superficie, una grandezza che ha a che fare con il percorrere (si fa più strada per andare da qui a lì o da qui a là? quanta strada occorre fare per tornare al punto di partenza in una linea chiusa?...); non ho mai creduto che i bambini possano confondere le due cose, e questo tanto più quanto più sono piccoli, ovvero quanto più sono vicini all’interazione percettivo-motoria con il mondo e quanto meno sono vicini al mondo dell’astrazione, dove l’interazione è veicolata dal linguaggio degli adulti. La mia conclusione è chiara: è il linguaggio usato dalle/dagli insegnanti a generare la confusione.
All’esempio citato sopra aggiungo che spesso l’insegnante nomina “quadretto” l’unità di misura di lunghezza più ovvia sul geopiano, ma anche sul quaderno (“la lunghezza del segmento è 4 quadretti”). Quando ci si riferirà all’area, cioè alla misura dell’estensione della superficie, di qualche “poligono” si dirà un numero seguito dall’unità di misura che sarà… “quadretti”. Naturalmente il prof. nella sua testa sa che questo “quadretto” è un quadratino, un pezzetto di superficie di forma quadrata, ma usa la stessa parola con cui prima ha indicato un’unità di lunghezza, corrispondente al lato del quadretto. Siccome l’alunno che riceve questa comunicazione non lo sa già (per questo è alunno e non insegnante), e non è tenuto a sapere che cosa ha in testa il prof., è normale che confonda “quadretto” con “quadretto”.

Un ultimo esempio:

RAPPRESENTA SUL GEOPIANO DUE SEGMENTI TALI CHE LA LORO SOMMA SIA 12

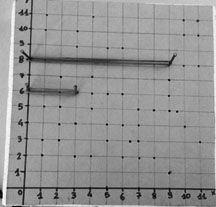La somma di due segmenti non può essere 12, per una ragione “ontologica”: 12 è un numero, mentre invece la somma di due segmenti è un segmento. È evidente che il prof. dice “somma di segmenti”, ma nella sua testa sta pensando a “segmenti che rappresentano graficamente due numeri e la loro somma” [vedi immagine 2, presentata dall’insegnante come risposta corretta, dove i due segmenti non sono adiacenti e quindi NON è rappresentata la loro somma]. Ancora una volta l’alunno dovrebbe rispondere a ciò che ha in testa il prof., ma non a ciò che comunica: è un cavillo solo se il contesto è una discussione al bar; è invece una questione fondamentale dal punto di vista ontologico, epistemologico ed educativo se il contesto è l’apprendimento della geometria e della teoria della misura. E ancora una volta una questione ontologica (che tipo di oggetto è un segmento? che cos’è la lunghezza?) convenzionata nelle “leggi della geometria” è molto utile per le competenze di cittadinanza, perché fornisce un linguaggio alle relazioni con la realtà (ad esempio si può percorrere un tratto di strada, non un numero; “misurare il percorso” non significa nulla: si può misurare la lunghezza del percorso, ma anche la sua inclinazione rispetto al Sole, o la sua pendenza rispetto all’orizzontale…
 

Riassumendo

La geometria è un sistema di enti astratti e di relazioni pensate tra questi enti. Quando si applica questo sistema mentale a un modello concreto lo si fa perché si pensa che la percezione e la manipolazione del modello possano aiutare la comprensione del sistema di idee. La condizione perché ciò accada è l’analogia tra sistema astratto e modello concreto.
Ma con il modello concreto si interagisce attraverso percezioni, che portano con sé elementi di non analogia. Gli oggetti materiali inevitabilmente hanno un sacco di caratteristiche che non hanno a che fare con la geometria o addirittura contrastano con le sue leggi convenzionate. In particolare il modello sta in uno spazio reale, tridimensionale e in più orientato dalla gravità, mentre per definizione convenzionata gli spazi geometrici non sono orientati, se non in modo relativo uno con l’altro. L’oggetto materiale geopiano di solito viene usato tenendolo in un piano orizzontale (il banco dello studente), quindi sia l’asse x che l’asse y sono entrambi orizzontali. Se il geopiano viene usato tenendolo in un piano verticale (la lavagna dell’insegnante), uno dei due assi è orizzontale e l’altro verticale, ma questo non ha alcuna importanza nel mondo della geometria, dove non esiste gravità e l’unico elemento pertinente è la posizione relativa dei due assi (perpendicolari tra loro o formanti un angolo diverso dall’angolo retto).
Non è un caso che all’inizio del ‘900 si sia pensato di eliminare i modelli grafici e visivi dalla geometria attraverso la rappresentazione cartesiana dove i punti sono coordinate, le relazioni spaziali sono funzioni, e i problemi di geometria sono equazioni (e uno spazio può avere un numero di dimensioni superiore a 3). È grazie a questo che un computer, che non “vede”, può “fare” geometria.
Si capisce allora che una operazione, che può essere decisiva per l’apprendimento della geometria come usare modelli visivi (e a maggior ragione materiali), sia un’operazione delicatissima, che richiede un assoluto rigore, innanzitutto nel linguaggio, che deve essere quello convenzionato per rispettare le leggi della geometria: non si può dunque assolutamente confondere gli oggetti con le grandezze e le grandezze con le misure. Anche l’insegnante più rigoroso non può mai perdere la consapevolezza di stare lavorando con un modello, ovvero con una analogia che ha i suoi due termini in mondi diversi, quello dell’astrazione convenzionata e quello della realtà fisica: sta veicolando significati astratti attraverso significanti materiali, che nella realtà percepita hanno relazioni che non corrispondono a quelle che hanno tra loro i significati. Se un insegnante non rispetta le leggi della geometria, se usa il linguaggio di un sistema di idee astratto senza tenere presente che sta applicandolo a un contesto concreto in cui si percepiscono e manipolano oggetti materiali, rende pressoché impossibile alle/ai bambine/i comprendere ciò che pretendeva di insegnare loro, cioè di che cosa è modello il modello.
Teniamo presente che i “cattivi” insegnanti non sono altro che quei bambini, cresciuti dentro questo gioco “truccato” che si perpetua lungo tutto il percorso scolastico. Stavo per usare il termine usuale di “curricolo verticale”, ma bisognerebbe essere consapevoli che si tratta solo di una metafora e che il curricolo, come il geopiano, non è soggetto alla legge di gravità.

 

 

Credits

---

Immagine a lato del titolo e immagine 1 tratte da "EmmaMetodo"